Код этого блога вместе с набором данных доступен по следующей ссылке https: // github.com / shekharpandey89 / k-means
Кластеризация K-средних - это алгоритм машинного обучения без учителя. Если мы сравним алгоритм неконтролируемой кластеризации K-средних с контролируемым алгоритмом, обучать модель с помеченными данными не требуется. Алгоритм K-средних используется для классификации или группировки различных объектов на основе их атрибутов или характеристик в K групп. Здесь K - целое число. K-среднее вычисляет расстояние (используя формулу расстояния), а затем находит минимальное расстояние между точками данных и кластером центроидов для классификации данных.
Давайте разберемся с K-средними на небольшом примере с использованием 4 объектов, каждый из которых имеет 2 атрибута.
| ObjectsName | Attribute_X | Attribute_Y |
|---|---|---|
| M1 | 1 | 1 |
| M2 | 2 | 1 |
| M3 | 4 | 3 |
| M4 | 5 | 4 |
K-средство для решения численного примера:
Чтобы решить указанную выше числовую задачу с помощью K-средних, мы должны выполнить следующие шаги:
Алгоритм K-средних очень прост. Сначала мы должны выбрать любое случайное число K, а затем выбрать центроиды или центр кластеров. Чтобы выбрать центроиды, мы можем выбрать любое случайное количество объектов для инициализации (зависит от значения K).
Основные шаги алгоритма K-средних:
- Продолжает работать до тех пор, пока никакие объекты не переместятся из своих центроидов (стабильно).
- Сначала мы случайным образом выбираем несколько центроидов.
- Затем мы определяем расстояние между каждым объектом и центроидами.
- Группировка объектов по минимальному расстоянию.
Итак, у каждого объекта есть две точки как X и Y, и они представлены в пространстве графа следующим образом:
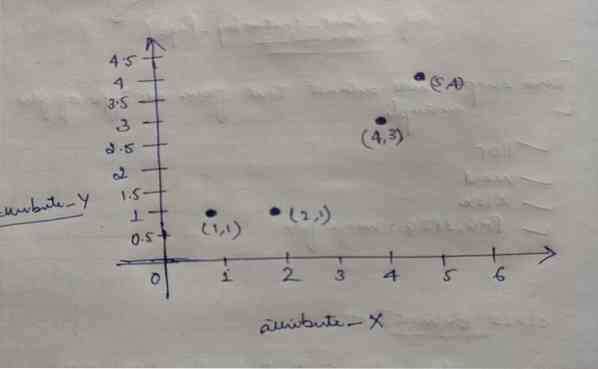
Поэтому мы изначально выбираем значение K = 2 как случайное, чтобы решить нашу вышеупомянутую проблему.
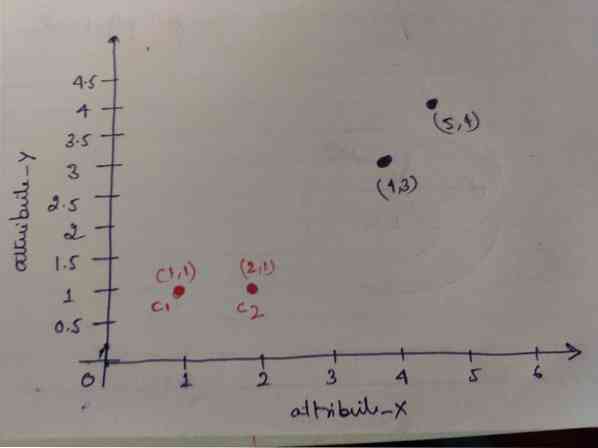
Шаг 1: Первоначально мы выбираем первые два объекта (1, 1) и (2, 1) в качестве наших центроидов. На графике ниже показано то же самое. Назовем эти центроиды C1 (1, 1) и C2 (2,1). Здесь мы можем сказать, что C1 - это группа_1, а C2 - это группа_2.
Шаг 2: Теперь мы рассчитаем каждую точку данных объекта относительно центроидов, используя формулу Евклидова расстояния.
Для расчета расстояния воспользуемся следующей формулой.

Мы вычисляем расстояние от объектов до центроидов, как показано на изображении ниже.

Итак, мы рассчитали расстояние до каждой точки данных объекта с помощью вышеуказанного метода расстояния, наконец, получили матрицу расстояний, как показано ниже:
DM_0 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) cluster1 | группа 1 |
| 1 | 0 | 2.83 | 4.24 | C2 = (2,1) cluster2 | группа_2 |
| А | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | Икс |
| 1 | 1 | 3 | 4 | Y |
Теперь мы рассчитали значение расстояния до каждого объекта для каждого центроида. Например, точки объекта (1,1) имеют значение расстояния до c1, равного 0, и c2, равного 1.
Поскольку из приведенной выше матрицы расстояний мы выясняем, что расстояние от объекта (1, 1) до кластера1 (c1) равно 0, а до кластера2 (c2) равно 1. Итак, объект 1 близок к самому кластеру 1.
Аналогично, если мы проверим объект (4, 3), расстояние до кластера 1 равно 3.61, а для кластера 2 - 2.83. Итак, объект (4, 3) переместится в cluster2.
Точно так же, если вы проверяете объект (2, 1), расстояние до cluster1 равно 1, а до cluster2 равно 0. Итак, этот объект переместится в cluster2.
Теперь по их значению расстояния группируем точки (кластеризация объектов).
G_0 =
| А | B | C | D | |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | группа 1 |
| 0 | 1 | 1 | 1 | группа_2 |
Теперь, согласно их значению расстояния, мы группируем точки (кластеризация объектов).
И, наконец, после кластеризации график будет выглядеть так, как показано ниже (G_0).
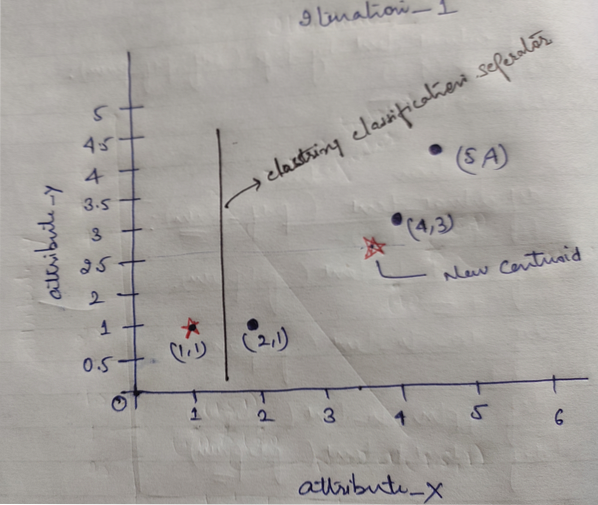
Итерация_1: Теперь мы вычислим новые центроиды, поскольку начальные группы изменились из-за формулы расстояния, как показано в G_0. Итак, у group_1 есть только один объект, поэтому его значение по-прежнему c1 (1,1), но у group_2 есть 3 объекта, поэтому его новое значение центроида равно 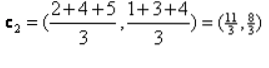
Итак, новые c1 (1,1) и c2 (3.66, 2.66)
Теперь нам снова нужно вычислить все расстояние до новых центроидов, как мы рассчитали ранее.
DM_1 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) cluster1 | группа 1 |
| 3.14 | 2.36 | 0.47 | 1.89 | C2 = (3.66,2.66) cluster2 | группа_2 |
| А | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | Икс |
| 1 | 1 | 3 | 4 | Y |
Итерация_1 (кластеризация объектов): Теперь, от имени вычисления новой матрицы расстояний (DM_1), мы сгруппируем ее в соответствии с этим. Итак, мы перемещаем объект M2 из группы_2 в группу_1 как правило минимального расстояния до центроидов, а остальная часть объекта будет такой же. Итак, новая кластеризация будет такой, как показано ниже.
G_1 =
| А | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | группа 1 |
| 0 | 0 | 1 | 1 | группа_2 |
Теперь нам нужно снова вычислить новые центроиды, так как оба объекта имеют два значения.
Итак, новые центроиды будут 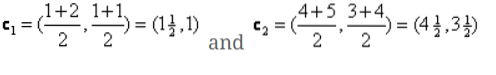
Итак, после того, как мы получим новые центроиды, кластеризация будет выглядеть следующим образом:
c1 = (1.5, 1)
c2 = (4.5, 3.5)
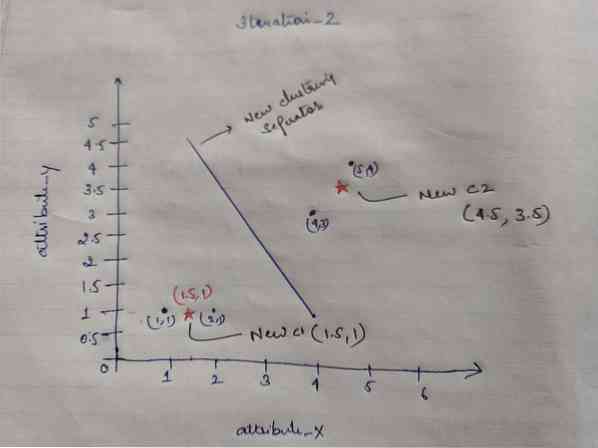
Итерация_2: Мы повторяем шаг, на котором мы вычисляем новое расстояние каждого объекта до новых рассчитанных центроидов. Итак, после расчета мы получим следующую матрицу расстояний для итерации_2.
DM_2 =
| 0.5 | 0.5 | 3.20 | 4.61 | C1 = (1.5, 1) cluster1 | группа 1 |
| 4.30 | 3.54 | 0.71 | 0.71 | C2 = (4.5, 3.5) cluster2 | группа_2 |
А Б В Г
| А | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | Икс |
| 1 | 1 | 3 | 4 | Y |
Опять же, мы выполняем назначения кластеризации на основе минимального расстояния, как и раньше. Итак, после этого мы получили матрицу кластеризации, которая такая же, как G_1.
G_2 =
| А | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | группа 1 |
| 0 | 0 | 1 | 1 | группа_2 |
Как здесь, G_2 == G_1, поэтому дальнейшая итерация не требуется, и мы можем остановиться на этом.
Реализация K-средних с использованием Python:
Теперь мы собираемся реализовать алгоритм K-средних на Python. Для реализации K-средних мы будем использовать знаменитый набор данных Iris с открытым исходным кодом. В этом наборе данных есть три разных класса. Этот набор данных имеет в основном четыре функции: Длина чашелистика, ширина чашелистика, длина лепестка и ширина лепестка. В последнем столбце будет указано имя класса этой строки, например setosa.
Набор данных выглядит следующим образом:
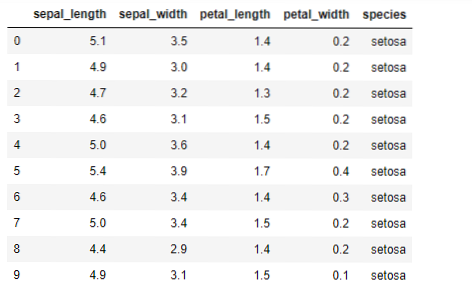
Для реализации python k-means нам нужно импортировать необходимые библиотеки. Итак, мы импортируем Pandas, Numpy, Matplotlib, а также KMeans из sklearn.clutser, как указано ниже:

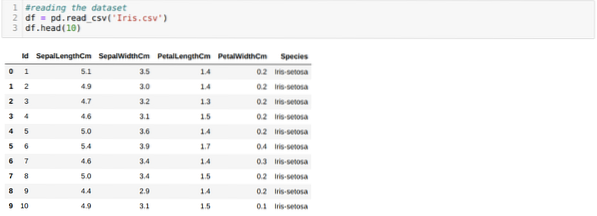
Читаем Ирис.csv с использованием метода read_csv panda и отобразит 10 лучших результатов с использованием метода head.
Теперь мы читаем только те функции набора данных, которые нам потребовались для обучения модели. Итак, мы читаем все четыре характеристики наборов данных (длина чашелистика, ширина чашелистика, длина лепестка, ширина лепестка). Для этого мы передали четыре значения индекса [0, 1, 2, 3] в функцию iloc фрейма данных панды (df), как показано ниже:
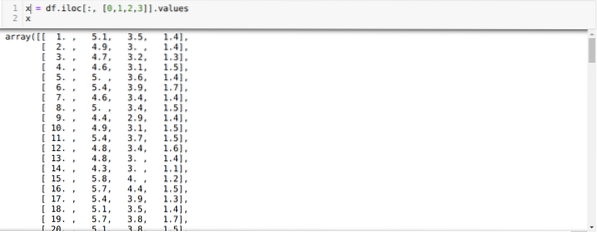
Теперь мы выбираем количество кластеров случайным образом (K = 5). Мы создаем объект класса K-means, а затем подгоняем наш набор данных x к нему для обучения и прогнозирования, как показано ниже:
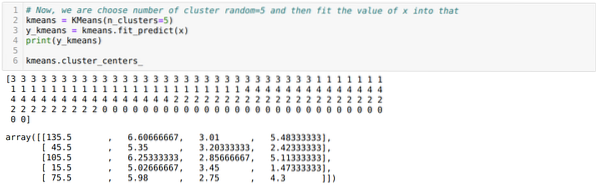
Теперь мы собираемся визуализировать нашу модель со случайным значением K = 5. Мы ясно видим пять кластеров, но похоже, что это неточно, как показано ниже.
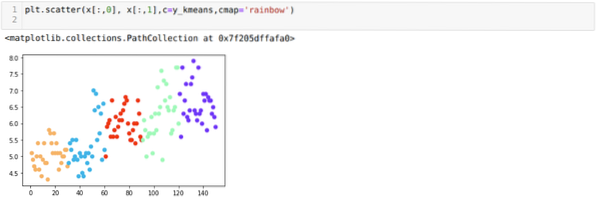
Итак, наш следующий шаг - выяснить, было ли количество кластеров точным или нет. И для этого мы используем метод локтя. Метод Elbow используется для определения оптимального количества кластеров для конкретного набора данных. Этот метод будет использоваться, чтобы выяснить, было ли значение k = 5 правильным или нет, поскольку мы не получаем четкую кластеризацию. Итак, после этого мы переходим к следующему графику, который показывает, что значение K = 5 неверно, потому что оптимальное значение находится между 3 или 4.
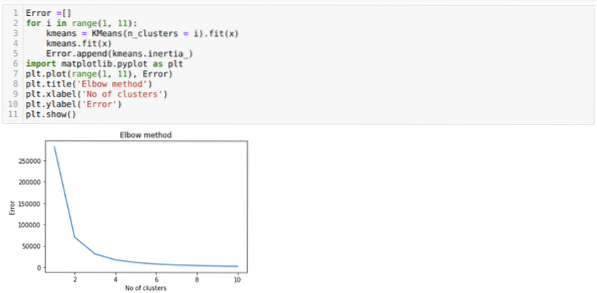
Теперь мы собираемся снова запустить приведенный выше код с количеством кластеров K = 4, как показано ниже:
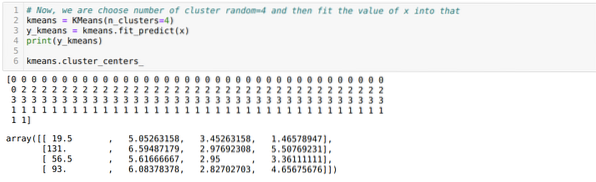
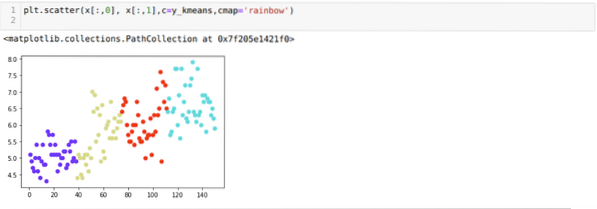
Теперь мы собираемся визуализировать вышеупомянутую кластеризацию новой сборки K = 4. На приведенном ниже экране показано, что теперь кластеризация выполняется с помощью k-средних.
Заключение
Итак, мы изучили алгоритм K-средних как в числовом, так и в Python-коде. Мы также видели, как можно узнать количество кластеров для определенного набора данных. Иногда метод Elbow не может дать правильное количество кластеров, поэтому в этом случае мы можем выбрать несколько методов.
 Phenquestions
Phenquestions


